Weighting the averages using Exponential Smoothing technique

The technique of exponential smoothing has many advantages over the moving average technique - it responds well to all sporadic demand changes. It takes more notice of the recent historical demand and less notice of the older demand data. Exponential smoothing technique provides a weighted average which improves the historical forecasting. It also doesn't need to have a very long periods of historical data as does the case in the moving average technique. The later gives equal importance to all the periods you want to evaluate, and also needs many recalculation each time.

You use exponential smoothing to derive a new forecast demand (which is in fact a historical "average"). The calculation is:

New Forecast = α x Demand in last period + (1-α) x Forecast for last period

α is the smoothing factor or constant.

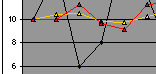
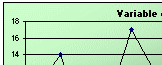
In Table 4.1, the calculation of new forecast using α =0.1 and α =0.3 respectively, analyses the last period's demand to give a historical average plus the remainder which we treated it as "statistical forecast fluctuation". The smoothing factor, α, defines the amount of notice which is taken of the each period's demand. The forecasts using exponential smoothing with α =0.1 and α =0.3 respectively, are calculated using the previous period's forecast. The MAD calculated in each case is 2.7 and 2.9 respectively, and this indicates that the statistical forecast using smoothing α =0.1 yields a better result. The chart on the right also indicates that the yellow line forecast with α =0.1 gives a much better smooth. [Download this worksheet]

Month	Last period demand	Forecast α = 0.1	Forecast Error1	Forecast α = 0.3	Forecast Error2		Figure 4.1
Jan-05	10	10.0	0.0	10.0	0.0
Feb-05	14	10.4	3.6	10.0	4.0
Mar-05	6	10.5	-4.5	11.2	-5.2
Apr-05	8	9.8	-1.8	9.6	-1.6
May-05	16	9.7	6.3	9.2	6.9
Jun-05	12	10.2	1.8	11.2	0.8
Jul-05	7	10.6	-3.6	11.4	-4.4
Aug-05	11	10.1	0.9	10.1	0.9
Sep-05	13	10.3	2.7	10.4	2.6
Oct-05	5	9.5	-4.5	11.2	-6.2
Nov-05	10	9.1	0.9	9.3	0.7
Dec-05	8	9.8	-1.8	9.5	-1.5
Sum of Absolute Forecast Error:			32.4		34.8
Mean Absolute Deviation (MAD):			2.7		2.9

Table 4.1 Exponential Smoothing technique

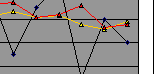
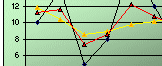
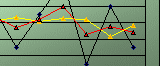
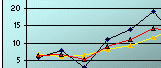
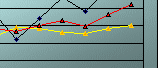
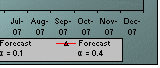
You can fine-tune the statistical forecast by altering the value of the smoothing constant (α). For effective exponential forecasting, the range of the smoothing constant which you can chose from are from 0.1 to 0.4. If the historical demand data varies slowly without sporadic changes, then α value of 0.1 or 0.15 is recommended. If there are understandable variable changes in average past demand level to which you want the forecast to smooth down the variability, a higher value of α, say, 0.4, should be chosen. In Figure 4.2 and Figure 4.3 below, which shows the much unstable variable demand and the increasing trend demand pattern, you see that the exponential smoothing with α =0.4 (the red curve lines) give a more reliable forecast in both cases. Remember this as the rule of thumb - low values of α make the forecast consistent; higher values of α make the forecast reactive to the variability of historical demand. However, smoothing with a higher value of α making your forecast rely too heavily upon demand in the last period.

In Figure 4.3, the variability of the demand was high from month to month and display an upward linear trend, using a low value of α smooth it to a more stable average as the yellow curve shows. However, if you have the more challenging customer service level goal to meet, you should use a higher value of α, say=0.4, as it reacts more rapidly to the trends in the past demand average level. MAD value of 4.1 shows that exponential smoothing using α=0.4 gives better forecast. If you have little knowledge or no idea of what caused the historical demand pattern of the part, then it is recommended to initially use a median value of α=0.2 or 0.25, then review the value of α again at regular periods on an on-going basis, and change the α value where necessary.

Download the following example worksheet.

Month	Historical Demand	Previous Forecast	Forecast α = 0.1	Forecast Error1	Forecast α = 0.4	Forecast Error2		Figure 4.2
Jan-06	10	12	11.8	-1.8	11.2	-1.2
Feb-06	14	10	10.4	3.6	11.6	2.4
Mar-06	5	9	8.6	-3.6	7.4	-2.4
Apr-06	8	9	8.9	-0.9	8.6	-0.6
May-06	17	9	9.8	7.2	12.2	4.8
Jun-06	12	10	10.2	1.8	10.8	1.2
Jul-06	7	11	10.6	-3.6	9.4	-2.4
Aug-06	11	10	10.1	0.9	10.4	0.6
Sep-06	15	10	10.5	4.5	12.0	3.0
Oct-06	5	11	10.4	-5.4	8.6	-3.6
Nov-06	12	8	8.4	3.6	9.6	2.4
Dec-06	7	10	9.7	-2.7	8.8	-1.8
Sum of Absolute Forecast Error:				39.6		26.4
Mean Absolute Deviation (MAD):				3.3		2.2

Table 4.2 exponential smoothing on a variable demand pattern

Month	Historical Demand	Previous Forecast	Forecast α = 0.1	Forecast Error1	Forecast α = 0.4	Forecast Error2		Figure 4.3
Jan-07	6	7	6.9	-0.9	6.6	-0.6
Feb-07	8	6	6.2	1.8	6.8	1.2
Mar-07	3	7	6.6	-3.6	5.4	-2.4
Apr-07	11	8	8.3	2.7	9.2	1.8
May-07	14	9	9.5	4.5	11.0	3.0
Jun-07	19	11	11.8	7.2	14.2	4.8
Jul-07	11	15	14.6	-3.6	13.4	-2.4
Aug-07	17	14	14.3	2.7	15.2	1.8
Sep-07	23	12	13.1	9.9	16.4	6.6
Oct-07	19	12	12.7	6.3	14.8	4.2
Nov-07	26	13	14.3	11.7	18.2	7.8
Dec-07	33	13	15.0	18.0	21.0	12.0
Sum of Absolute Forecast Error:				72.9		48.6
Mean Absolute Deviation (MAD):				6.1		4.1

Table 4.3 exponential smoothing on a increasing trend demand pattern