About Me
Excel VB Programming (VB6)
Excel Spreadsheet Formulas
Excel VB.NET Programming
Access Programming (2003)
Safety Stock Planning
The main reason of keeping safety stock is to buffer against random fluctuations in demand. Other reasons are because of the unreliability of supply and long transportation lead time. With improvements in product quality, supplier's lead time and logistics infrastructure, the last two factors can become relatively insignificant. Uncertainty in customer's demand can be dealt with using forecasting techniques.
The random variations in demand usually follow a 'normal' or Gaussian distribution which is the idealized distribution for a very large number of periods of demand. Statistical safety stock can be calculated using 'normal' distribution. Such is a statistical technique which planners often question its validity, comparing it to the practicality of their work experience, but it can be quite helpful for management in terms of deciding the safety stock investment level.
Customer service levels
Safety stock level has a direct impact on customer service level. There are two types of Customer Service you can use - one with regards to safety stock and another with regards to order fulfillment.
-
Safety stock customer service level refers to the percentage of the numbers of orders received without a stock-out compared to the total exposures to stock-out. Some companies call it "Target safety stock fill-rate" which they report on a weekly or monthly basis. For example, customer placed a total quantity of 10 orders at different times for the month, and there was one incident of stock-out bin on the date required delivery should be sent, the safety stock customer service level therefore will be [(10-1)/10] which is 90%.
-
Demand fulfillment customer service level refers to the percentage of demands filled within an agreed time frame based on customer's total required quantity and required date. In another word, it is the number of satisfied demands divided by the total number of demands. It can be measured in the form of either by item quantities or by the number of line items, and within 12 hours, 24 hours, 48 hours or whatever, depends on the agreement that you have reached with the customer.
[see this example].
Do you really need a safety stock? Some managers like to think that the inventory that are not issued in periods when demand is less than forecast, can be used to "offset" demand during periods when actual demand is higher than the forecast. Thus they think that on average safety stock is not intended to be used. For every part which dips into safety stock level due to under-forecast, they argue that there is also a part which does not consume its forecasted quantity. They want to save on safety stock investment and explain any potential service level dip to customers by pointing it to forecast inaccuracy. However, such is a mistaken belief that company does not need any safe stock because high and low demand periods only net to the forecast over a long period of time as is with normal distribution assumption, and also variability averages out only when the forecast tracks actual demand fairly closely. In the short term, every period with low demand does not follow with a period of high usage. Only in periods of ascending demand does high usage follows one another. Therefore, there are cases when having safety stock is the only option to meet your target customer service level.
An important aspect of safety stock with respect to customer service level is that, the number of stock-outs per month that the company faces is relatively unimportant when comparing to the number of days of stock-out of a critical part that the customer experiences. A single item stock-out per year may seem like much for a company. A stock-out period of 7 days may mean a week of lost production, rescheduling, overtime costs or lost sales to your customer if the the stock-out part affects a constrained operation.
Over-planning of Master Production
Schedule
Sometimes because of
continuous higher forecast and demand, the master scheduler may over-plan
certain products so that when actual usage occurred higher than the forecast,
there is always some extra sets of inventory that is available to meet the
increased demand. Companies don't normally produce these extra products unless
there is a demand. Over-planning at master schedule level will produce extra
sets of parts or sub-assemblies based on their levels in the bill of material.
For simplicity for example, let's assume a unit of product 123C requires 15
pieces of part A and 8 pieces of sub-assembly B. Product forecast for the month
was planned at 30 units, and you planned 20% extra of part A and 5% extra of
sub-assembly B. If the actual demand was 25 units, the effect of over-planning
at master schedule level produces excess safety stock of 165 pieces for
part A and excess 26 sub-assemblies B. [see more detail in this
worksheet].
When demand dips and you have this kind of excess safety stock or inventory, you
should know who to be held responsible for.
Calculating statistical and fixed safety stock
There are two primary techniques commonly used to set a safety stock level - statistical (using standard deviation and mean absolute deviation) and fixed techniques. I will explain them later. The choice of selecting which technique to use depends on the type of part (dependent- or independent-demand), type of demand of the part (stable or sporadic), its degree of variability (high or low), replenishment lead time of the part, availability of at least 6 to 12 months of historical usage data, and the target customer service level commitment. A point to note is that planners must be aware of the products and parts in their different stages of the product life cycle, and not just relegate to the computer by taking in everything what the statistical technique calculated for them. They must still check on the validity of the statistical calculation for some important categories of parts.
Which parts exactly of the unplanned usage that caused stock-out situation that are unacceptable to the customers? How can you know exactly which parts of of the unplanned usage that must be protected by safety stock to prevent causing another very unhappy customers? One way is to look at the product life cycle stages. For new products in the introduction and growth stages, there is little risk in stocking enough materials to meet high customer service levels since the materials will continue to have demand in the short term. The primary danger planners must pay attention to in the introduction and growth stages is that certain categories of parts may be superseded by another part through engineering changes if the product is encountering quality issues or still undergoing modifications. Under such circumstances, parts may be phased out, can not be sold or used in another product, or service parts become excess, surplus, inactive, and eventually become obsolete and have to be scrapped. Finance managers usually aren't very tolerating when inventory dollars has to be written off due to poor planning and mismanagement.
Product in the maturity phase usually see high demand of parts and companies are often asked to keep more safety stock to meet customer service level. It is in this phase inventory planners face the greater challenge of keeping inventory costs down while continue to sustain customer service performance. The pressure is on reducing safety stock investment, free up cash flow while relying upon production volume and product lines mix flexibility to make up for any unplanned demand.
A fixed safety stock approach is normally used under the following situations:
-
a new part is being phased in during the product introduction stage. Because there is insufficient historical demand data, a calculated safety stock may be too low. Establishing a fixed safety stock prevents the new part from stock-out during NPI (New Product Introduction) phase. Take not that a replacement or substitution part which supersedes another is not the same. Your inventory system should already take into account the historical usage of the old part that was substituted to provide sufficient calculated safety stock quantity.
-
a part may be phased out, taken out of the bill-of-material, becomes inactive and excess. Demand will gradually tail off as demand softens, and as the Program manager tries to offer price breaks to customers in order to deplete the excess on-hand balance before the parts reach shelf-life expiry dates. Under such situation planners should set the fixed safety stock level to zero, and monitor the on-going usage.
-
Dependent-demand parts are planned through the Master Schedule (MS) and MRP systems. This is usually planned in a production or assembly environments where there are no unplanned usage like customers placing direct orders. The material planner should flag the safety stock technique to "fixed" and safety stock quantity to zero.
There are two common types of measurements to find the variability of the supply and demand, namely Standard Deviation and Mean Absolute Deviation. In essence, they are just the two different ways of measuring the same thing.
Calculating the standard deviation (σ)
Standard deviation (σ) is a measure of the spread of a probability distribution or how widely values are dispersed from the average value (the mean). Consider two parts that have the same forecasted usage rate. The one which experiences the greater deviation of the actual usage rate from the forecasted usage rate will have a greater spread. The smaller the standard deviation, the higher the probability of the actual usage rate tracking closely to the forecasted usage rate. You can also see from the explanation note of 'normal distribution' where actual demand is approximating the forecast with each additional decrement of the standard deviation (or sigma).
Mathematically, standard deviation (σ) is calculated as:
| SD = | 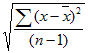 |
which is the square root of the
sum of the forecast deviations squared divided by the number of periods - 1. (n
is the number of periods, and x-
![]() is the forecast deviation).
is the forecast deviation).
Table 4.1 below contains the forecast and actual demand for a 12 months period, which are used to calculate 4 types of deviations in five columns. [you can download the worksheet workout with the formula].
| Sum of Forecast Deviation squared |
=
|
| = SUM(E3:E14) | |
| = 1450 | |
| Standard Deviation (σ) |
= SQRT(1450/(12-1)) |
| = 11.48 pcs | |
| Absolute Deviation | = ABS[Forecasted Usage - Actual Usage] |
| Absolute Deviation for Feb. | = ABS(100-105) |
| = 5 pcs | |
| Sum of Absolute Deviation | = ABS(SUM(ABS(D3:D14))) = 110 pcs |
| note: this must be entered as an array formula. Press Shift+Ctrl+Enter. | |
| Mean Absolute Deviation (MAD) | = Sum of the absolute deviations/number of periods |
| = 110/12 = 9.17 pcs |
Table 4.1 Calculating Standard Deviation and Mean Absolute Deviation
You may ask why should include the deviations with actual demand less than forecast since stock stock had not been used in those periods. This is because the calculations of standard deviation and mean absolute deviation both consider under-deviations and over-deviations (+ and - signs). All the forecast deviations must be summed using Absolute values and then averaged in order to obtain a representative deviation. Forecast deviation columns are used to calculate σ and MAD. Over-deviation column calculates only over-deviation of actual demand above forecast.
Calculating the Mean Absolute Deviation (MAD)
Mean Absolute Deviation (MAD), like SD ( or σ), is a simple assessment of the variability of the demand pattern, a basis from which safety stock can be calculated. You can consider MAD as a percentage of the demand variations over a given number of periods into the past. For a normal distribution, MAD =0.8 standard deviation. For improved safety stock calculation, the assessment of the variability between forecast and actual demand must use the most recent data, and the value should be exponentially weighted [see weighted averages using Exponential Smoothing technique]. Calculating MAD is easier than standard deviation (SD) because you have to convert SD to variance (SD2) in using exponential weighting technique. Exponentially weighted MAD is also more effective than SD, especially useful in seasonal demand, and giving improved safety stock levels.
In Table 4.1, MAD is calculated as:
|
MAD |
= |
Sum of the absolute deviations from mean |
| Number of periods | ||
|
|
= | 110/12 |
| = | 9.17 pcs |
You can fine-tune the exponential forecast by adjusting the value of the smoothing constant (α). For effective exponential forecasting, the range of the smoothing constant which you can chose from are normally 0.1 to 0.4. If the historical demand varies slowly with not much variations, you should use a lower α value of 0.1. If value of α=0.1 makes the new forecast a little insensitive to demand level, then use α=0.15. If there are variable changes in the average past demand level to which you want the forecast to smooth, you should use a higher value of α, say, 0.4.
In Table 4.1, MAD for Jan using the weighting factor α=0.2 is calculated as:
| New MAD (Jan) | = (α x Absolute Deviation) + ([1 - α] x old MAD) |
| = (0.2*ABS(D3))+((1-0.2)*G2) which is also, | |
| = (0.2 x 20) + ((1 - 0.2) x 9.17) | |
| = 11.34 pcs |
MAD for Dec using the weighting factor α=0.5 is calculated as:
| New MAD (Dec) | = (0.5*ABS(D14))+((1-0.5)*H13) which is also, |
| = (0.5 x 5) + ((1 - 0.5) x 8.42) | |
| = 6.71 pcs |
In Table 4.1, The α=0.2 smoothed MAD was lower than the non-weighted MAD in December by about 12%, that is ((9.17-8.04)/9.17). The α=0.5 smoothed MAD was about 27% lower. The two MAD equations using 0.2 and 0.5 Alpha Factor also recognized that the 15 to 20 magnitude forecast deviations of the demand occurred further in the past prior to July, and all the more recent deviations from July onward were all in the 5 to 10 deviations range. Both 0.2 and 0.5 Alpha Factors reacted at the time of the larger deviations. Over time, however, the smaller 5 to 10 magnitude deviations caused the smoothed MAD to be reduced. The conclusion here is that the non-smoothed MAD technique weighted all periods equally, without accounting for the newer or the older periods of the data. However, the MAD smoothing technique with Alpha (α) Factors reacted more heavily to the more recent trend toward lower deviations
Calculating statistical safety stock using MAD
It involves many mathematical computations and for this it is best to illustrate with an example. Consider the following:
| 60 days | :Lead time (assuming 20 workdays per month) |
| 90% | :Target safety stock service level |
| 0.20 | :Weighting factor (σ) |
| 40 pcs | :Order qty |
| 125 pcs | :Last month's actual usage rate |
| 100 pcs | :Last month's forecasted usage rate |
| 1.00 |
:Old MAD |
| Absolute Deviation | = ABS[Forecasted Usage - Actual Usage] |
| = 100 - 125 | |
| = 25 pcs | |
| New MAD | = (σ x Absolute Deviation) + ([1 - σ] x old MAD) |
| = (0.20 x 25) + ((1-0.20) x 1.00) | |
| = 5.8 pcs | |
| In
calculating MAD, the same as was shown previously in
exponential smoothing technique - the
higher the value of the smoothing alpha factor, the more weight is given
to the most recent data than to deviations in the older periods. Standard Deviation is used as a reference for statistical tables which are based on the standard deviations. Some computerized inventory system automatically calculates the standard deviations for you, based on the past lead times experienced. SD can be approximated as: |
|
| Standard Deviation | = MAD x 1.25 |
| = 5.8 x 1.25 | |
| =7.25 pcs | |
| Lead Time Deviation | = Standard Deviation x (Lead Time in months/Forecast period)β |
| (base on SD) | = 7.25 x (3)0.5 which is =7.25*POWER(3,0.5) in your Excel spreadsheet |
| = 7.25 x 1.732 | |
| = 12.56 pcs | |
| Lead Time Deviation | = MAD x (Lead Time in months/Forecast period)β |
| (base on MAD) | = 5.8 x (3)0.5 which is =5.8*POWER(3,0.5) in your Excel spreadsheet |
| = 5.8 x 1.732 | |
| = 10.05 pcs | |
|
The calculation of Lead Time Deviation extends the standard deviation
over some portion of the lead time for parts which have a forecast
review period that does not match the total replenishment lead time of
the parts. The calculated standard deviation is based on a 1-month
forecast period, but the part has a 3-month lead time.
Theoretically, a situation may occur such that the part that you have
released for purchase order may experience 3 months in a row of higher
than forecasted demand. The calculated safety stock under such
worst-case scenario would assume that the average deviation would occur
for 3 months in a row. Therefore Lead Time Deviation formula applies a
beta factor (β) to account for some portion of the deviation over the
lead time. Beta factor (β) is typically set in the 0.5 to 0.7 range. 0.5
is commonly used. Setting to 1 is equivalent to the worst-case scenario. Table 4.2 is a Normal Distribution function table which shows the Safety Factors based on a Normal Distribution. Safety Factor in short is for "customer safety stock service factor". Safety Factor is the number of Standard Deviations (or MAD) associated with the Safety Stock Service Level Percent. Your computerized inventory system has its own lookup information table that looks something like Table 4.2 to assign the Safety Factor. Given that the target safety stock service level is 90% and if you look at Table 4.2 the Safety Factor is 1.28 based on σ (or equal to 1.60 based on MAD). Therefore you now can calculate the statistical safety stock either using 1.28 or 1.60. |
|
| Statistical Safety Stock | = Safety Factor x Lead Time Deviation |
| = roundup((1.28*12.56),0) | |
| = 17 | |
| or using 1.60 based on MAD | |
| Statistical Safety Stock | = roundup((1.60*10.05),0) |
| = 17 | |
| Desired Safety Stock Service Level (% periods without stockout) | Additional Safety Stock Service Percent from statistical table | Safety Factor for Standard Deviation (σ) |
Safety Factor for MAD (σ x 1.25) |
| 50.00% | 50.00% | 0.00 | 0.00 |
| 80.00% | 79.95% | 0.84 | 1.05 |
| 85.00% | 84.13% | 1.00 σ | 1.25 |
| 90.00% | 89.97% | 1.28 | 1.60 |
| 94.52% | 1.60 | 2.00 | |
| 95.00% | 95.05% | 1.65 | 2.06 |
| 97.72% | 2.00 σ | 2.50 | |
| 98.00% | 97.98% | 2.05 | 2.56 |
| 99.00% | 99.01% | 2.33 | 2.91 |
| 99.18% | 2.40 | 3.00 | |
| 99.87% | 3.00 σ | 3.75 | |
| 99.93% | 3.20 | 4.00 | |
| 100% | 99.99685% | 4.00 σ | 5.00 |
| 99.99997% | 5.00 σ | 6.25 | |
| 99.999999% | 6.00 σ | 7.50 | |
|
|
|||
|
Table 4.2 Safety Factors based on a Normal Distribution |
|||
Planners need to specify the number of sigma accounts for the 100% customer service level by part. Although the default is 4 σ for 100% service, the actual may be from 3 to 6 σ based on the actual deviations experienced in the past.
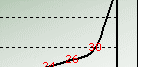
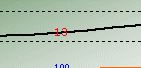
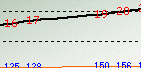
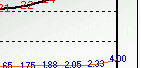
Now we come to the more interesting part. With the calculated σ, new MAD, Lead Time Deviation and the known Safety Factor (based on σ or MAD) in this example, we can associate the quantity of safety stock with the various customer safety stock percents (tabulated in Table 4.3). Safety Factor is related to the safety stock replenishment frequency as you can see from the graph that with every increment of Safety Factor, you are increasing the safety stock quantity which in turns provides you improved Safety Stock Service Percents, of course, less stockout.
| Customer Safety Stock Service Percents | ||||||||||||
| Safety Stock Service % | 80% | 85% | 89% | 90% | 93% | 94% | 95% | 96% | 97% | 98% | 99% | 100% |
| SD (σ) | 7.25 | 7.25 | 7.25 | 7.25 | 7.25 | 7.25 | 7.25 | 7.25 | 7.25 | 7.25 | 7.25 | 7.25 |
| New MAD | 5.8 | 5.8 | 5.8 | 5.8 | 5.8 | 5.8 | 5.8 | 5.8 | 5.8 | 5.8 | 5.8 | 5.8 |
| Lead Time Deviation (β=0.5) | 12.56 | 12.56 | 12.56 | 12.56 | 12.56 | 12.56 | 12.56 | 12.56 | 12.56 | 12.56 | 12.56 | 12.56 |
| Safety Factor (based on σ) | 0.84 | 1 | 1.25 | 1.28 | 1.5 | 1.56 | 1.65 | 1.75 | 1.88 | 2.05 | 2.33 | 4 |
| Statistical Safety Stock | 11 | 13 | 16 | 17 | 19 | 20 | 21 | 22 | 24 | 26 | 30 | 51 |
|
Table 4.3 Deriving Safety Stock Level at the various Safety Stock Service Percents |
||||||||||||
You can download Table 4.3 with the plotted graph as shown below.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Non-smoothed calculation | Based on 0.2 Alpha Factor | Based on 0.5 Alpha Factor | |||
| Old MAD | N/A | 8.80 | 8.42 | ||
| New MAD | 9.17 | 8.04 | 6.71 | ||
| SD (New MAD x 1.25) | 11.46 | 10.05 | 8.4 | ||
| Lead Time Deviation (β=0.5) | 19.85 | 17.41 | 14.52 | ||
| Safety Factor based on SD (α) | 1.28 (90%) | 1.28 (90%) | 1.28 (90%) | ||
| Statistical Safety Stock | 26 | 23 | 19 | ||
| Safety Stock % reduction | 11.5% | 26.9% | |||
Table 4.4 Comparing the Safety Stock Level at different New MAD calculations.
Table 4.4 is derived from Table 4.1 in the previous example. Table 4.4 compares the safety stock level required based on the different calculated value of the three MADs, SD, Lead Time Deviation with β=0.5 and 3-month replenishment lead time, and Safety Factor of 1.28 at 90% customer safety stock service level. Based on Alpha factor 0.2, there is 11.5% less safety stock [(26-23)/26] required than using the non-weighted calculation. Using 0.5 Alpha factor results in about 27% lesser [(26-19)/26]. You can see all the calculations in this worksheet.
Next
Page >>
Economic Order Quantities