Exponential Smoothing With Seasonality Methods

If you look at Table 4.1, you see that there is a systemic error pattern occurs every fourth period (negative values). Only there is an exception at period 21 where there are twice negative values, because of randomness. Using Winter's method would be able to eliminate this kind systematic pattern in the errors. Winter's method is based on three smoothing equations - St for overall smoothing, bt for trend, and Ot for seasonality.

Table 4.1 shows applying the earlier three smoothing methods that had been discussed, to a seasonal data series. Looking at the descriptive statistics summary, it appears that the Holt's three-parameter smoothing method gives the smallest errors (MAE=72.80, MAPE=13.09, MSE=7265.55, and the standard deviation of errors is giving 85.24). However, there is too much smoothing that is done, and the every fourth-month periodic systemic errors also need to be eliminated. Clearly, we require the Winter's method to improve it, as shown in Table 4.2. The descriptive statistics in Table 4.2 shows that Winter's method gives the smallest errors among the four methods (MAE=28.61, MAPE=5.41, MSE=1102.76, standard deviation of errors =33.21).

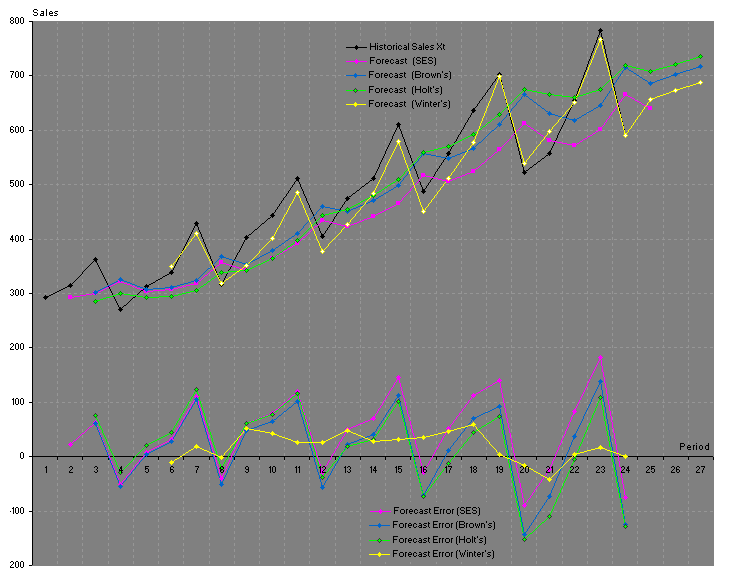
In Figure 4.1, the Winter's method is super-imposed over the other three methods versus the original observed series. The original data clearly shows a linear trend with additive seasonality. The seasonal cycle repeats in almost every four periods. The Winter's method shows that the forecast (the yellow curve) trails the original data closely and yet not overly smoothed as was the case in the other three methods.

To initialize the Winter's forecasting method, we need to use at least one complete season's data (i.e., L periods =4) to determine the initial estimates of the seasonal indices, Ot-L. Let S3=X2 and calculate the single smoothing value for S4 base on S3=X2. The initial value of the Trend factor, b4, can be calculated using the following method:

Each of the terms as in above, until (XL+4 - X4) / L, is an estimate of the trend over the complete season (L=4).

Other methods for initializing can be created and their influence on later forecasts will depend on the length of the time series and the values of the three parameters.

Initializing values:

S3 =S2

S4 =S3 + [0.2 * (X3 - S3)]
=315 + (0.2 * (362 - 315))   =324.40

O1 =[X1 / (X1 + X2 + X3 + X4) / 4]

=[292 / (292+315+362+271)/4]   292/310   =0.942

O4 =271/310 =0.874

b4 =[(X5 - X1)/4 + (X6 - X2) / 4 + (X7 - X3)/4 + (X8 - X4) / 4] / 4

=(5+6+16.5+11.5)/4   =9.75

Calculating the test set:

S24 =0.2 (X24 / O20) + 0.8 (S23 + b23)

=0.2*(591/0.878) + 0.8*(655.22+17.03)   =672.41

b24 =0.1(S24-S23) + 0.9(b23)

=0.1*(672.41-655.22)+0.9*(17.03)   =17.05

O24 =0.05(X24/S24) + 0.95(O20)

=0.05*(591/672.41)+0.95*(0.878)   =0.878

F24 =[S23 + b23 (1)] * O20   =(655.22+17.03(1))*0.878   =590.34

F27 =[S24 + b24 (3)] * O21   =(672.41+17.05(3))*0.952   =688.64

You can download the worksheet to have a better feel of the formula.

Figure 4.1 Application of Single Exponential Smoothing, Linear 2-Parameter and Linear 3-Parameter Smoothing,
and Winter's Linear and Seasonal Exponential Smoothing To Seasonal Sales Data

One of the problems in using Winter's method is in determining the values for the three parameters - , and that will minimize MSE or MAPE. The correct way to do this is to change the values of the parameters in their respective cells in Excel, and then observe the changes in the line graphs which you would have already plotted next to the spreadsheet table. An alternative is to write a Visual Basic macro to run through the upper and lower bound values you will set for the 3 parameters, and populate the return forecast values in a one or a few columns. Once the forecasts are done, you can plot the graphs to see the trend and smoothing effect after re-adjusting each of the range one at a time. Either way, it can be quite time-consuming.

Winter's method is just one of the several exponential smoothing methods that can handle linear trend and seasonality. There are other methods that can handle linear trend, and multiplicative seasonality.

Go To Top